Ball and Beam (ballbeam)¶
A beam is pivoted on a bearing in its middle. The position of a ball on the beam is controlable by applying a torque into the bearing.
The ball has a mass 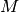 , a radius
, a radius 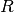 and a moment of inertia
and a moment of inertia 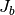 .
Its distance
.
Its distance  to the beam center is counted positively to the right.
For the purpose of simplification, the ball can only move in the horizontal direction.
to the beam center is counted positively to the right.
For the purpose of simplification, the ball can only move in the horizontal direction.
The beam has a length 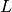 , a moment of inertia
, a moment of inertia 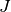 and its deflection from the horizontal line is the angle
and its deflection from the horizontal line is the angle 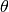 .
.
The task is to control the position  of the ball with the actuation
variable being the torque
of the ball with the actuation
variable being the torque 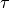 . The interesting part in this particular
system is that while being nonlinear and intrinsically unstable, it’s relative
degree is not well-defined. This makes it an exciting but yet still clear lab
example. The description used here is taken from the publication [Hauser92] .
. The interesting part in this particular
system is that while being nonlinear and intrinsically unstable, it’s relative
degree is not well-defined. This makes it an exciting but yet still clear lab
example. The description used here is taken from the publication [Hauser92] .
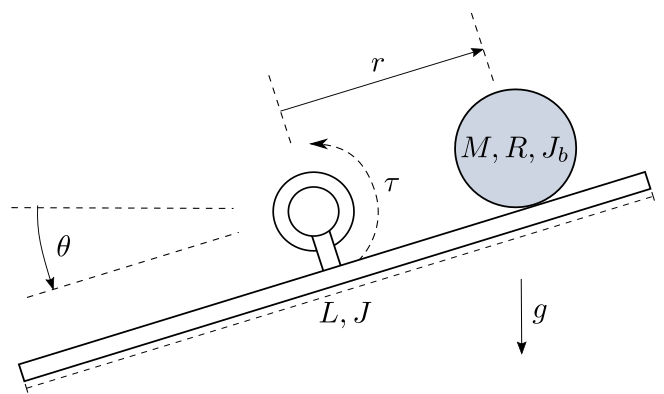
Fig. 9 The ball and beam system
With the state vector
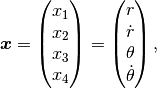
the nonlinear model equations are given by
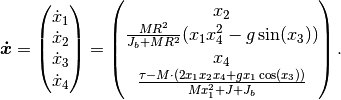
Violations of the model’s boundary conditions are the ball leaving the beam
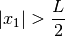
or the beam’s deflection reaching the vertical line
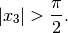
The ball’s position
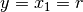
is chosen as output.
The example comes with five controllers.
The FController and GController both implemenent a input-output-linearization of the system
and manipulate the second output derivative by ignoring certain parts of the term.
The JController ignores the nonlinear parts of the linearized model equations,
also called standard jacobian approximation.
The LSSController linearizes the nonlinear model in a chosen steady state
and applies static state feedback.
The PIXController also linearizes the model and additionally integrates the control error.
LinearFeedforward implements a compensation of the linear system equation parts,
with the aim of reducing the controllers task to the nonlinear terms of the equations and disturbances.
The example comes with four observers.
LuenbergerObserver, LuenbergerObserverReduced and LuenbergerObserverInt
are different implementations of the Luenberger observer.
The second of these improves its performance by using a different method of integration and the third uses the solver for integration.
The HighGainObserver tries to implement an observer for nonlinear systems,
However, the examination for observability leads to the presumption that this attempt should fail.
A 3D visualizer is implemented. In case of missing VTK, a 2D visualization can be used instead.
An external settings file contains all parameters.
All implemented classes import their initial values from here.
At program start, the main loads two regimes from the file default.sreg.
test-nonlinear is a setting of the nonlinear controller moving the ball from the left to the right side
of the beam.
test-linear shows the step response of a linear controller, resulting in the ball moving from the middle to the right side of the beam.
The example also provides ten different modules for postprocessing.
They plot different combinations of results in two formats, one of them being pdf.
The second format of files can be given to a metaprocessor.
The structure of __main__.py allows starting the example without navigating to the directory
and using an __init__.py file to outsource the import commands for additional files.
| [Hauser92] | Hauser, J.; Sastry, S.; Kokotovic, P. Nonlinear Control Via Approximate Input-Output-Linearization: The Ball and Beam Example. IEEE Trans. on Automatic Control, 1992, vol 37, no. 3, pp. 392-398 |